JOrigami Computational Origami Algorithms in Java

" Most models have their structures. You should understand them. And find out the best sequence. Change some folds if necessary. You don't have to follow the diagrams. Origami Tips, Hatori Koshiro

Download release here | Source code here | Beautiful SVGs here

What is this?

This is an open source java implementation for the fold and cut problem (a pretty old problem). It can be stated as this: cosidering a polygon as the input, can we fold a paper in such way that with an straight cut it will generate the given polygon? The fantastic answer here is YES, for any polygon. And here we have implemented one solution for this problem. The generated origamis can be really hard to fold.

David Eppstein, one of the authors of the paper that describes the algorithm used here, bloged about us. Thanks David. Also thanks for Marshal Bern and Barry Hayes, who spent some time with our emails.

To get a better understanding of Computational Origami and the fold-and-cut problem, you can take a look at these papers:

• On the Mathemathics of Flat Origami, Thomas Hull
• When Can you fold a Map?, Erik Demaine, Esther M. Arkin, Michael A. Bender, Martin L. Demaine, Joseph S. B. Mitchell, Saurabh Sethia and Steven S. Skiena
• Complexity of flat Origamis, Marshal Bern and Barry Hayes
• A computational algorithm for Origami Design, Robert J Lang
• A Disk-Packing Algorithm for an Origami Magic Trick, Erik Demaine, Marshal Bern, Barry Hayes and David Eppstein

There is also a book being written by Demaine and O´Rourke called Geometric Folding Algorithms: Linkages, Origami, and Polyhedra, (formerly know as Folding and Unfolding in Computational Geometry, a more charming title). A whole chapter is dedicated to the fold-and-cut problem.

The implementation uses voronoi diagrams concepts, appollonious problems, universal molecules, modified winged edges, lots of computational geometry primitives, packing heuristics, face manipulations and much more, making it pretty interesting and challenging.

All images here are available as svg. You can download them here. The software can also take svg screenshots (just press screenshot!).

The big fish: step by step

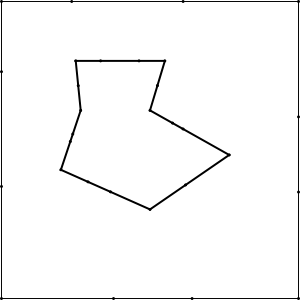
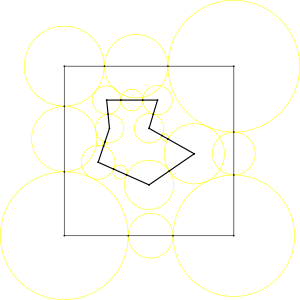
Polygon, Initial disk positioning (automatic, it can be done manually), Full edge coverage.

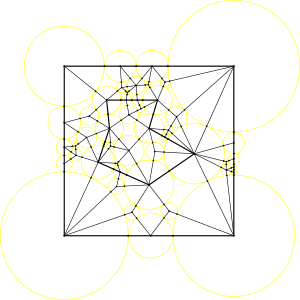
Fixed edge coverage and splitted faces, Partitioning in quadrilaterals and triangles, The tree

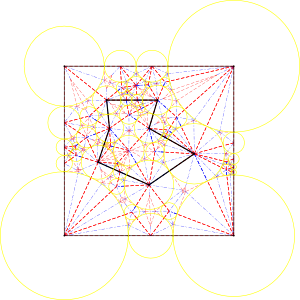
Crease pattern, Crease pattern with fixed M-V assignment, crease pattern and disks

A star

The same star, not centered

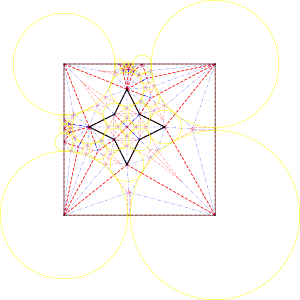
Manual initial packing, Biggest Neighbor, 474 folds. Min distance, Median disk, 564 folds. No initial optimization, biggest neighbor, 1184 folds.

The size of the paper can make a huge difference, but the molecules that do not touch the polygon do not need to be folded.

Other cool images

Contact